AFT Blog
Let the Heat Flow: Modeling Heat Transfer in Pipes in AFT Fathom and AFT Arrow
Among the many talents of AFT Fathom and AFT Arrow software is the ability to model heat transfer. While a major source of heat transfer is heat exchangers, this blog will address heat transfer that occurs in pipes.
First, for the basics: Just what is heat transfer? Well, heat transfer occurs when there is a temperature difference between two objects at different temperatures. As all engineers know, the common theme of physics is that matter and energy alike travel spontaneously from higher, more chaotic surroundings to calmer, lower energy situations (not unlike the stereotypical engineer), and heat transfer is no different. Just like in fluid mechanics when fluid flows from higher head to lower head, or in spontaneous chemical reactions when two molecules bind in an exothermic reaction, heat transfer tends towards establishing an equilibrium. This means that heat flows from high temperatures to low temperatures.
There are different types of heat transfer. The two types of heat transfer that AFT Fathom and AFT Arrow explicitly model include conduction and convection. Conduction is the transfer of heat via direct physical contact, while convection is the transfer of heat via the mass motion of a fluid. Radiant heat flux can be modeled with the constant heat flux model in AFT Fathom and Arrow.
Isothermal: The isothermal heat transfer model maintains the pipe temperature at the user-input temperature. While often confused with adiabatic heat transfer, the significance of isothermal heat transfer is slightly different because the temperature is actively maintained at the specified temperature. In AFT Fathom, isothermal pipes are only very slightly different from adiabatic pipes because isothermal pipes use the input temperature at the pipe, whereas adiabatic pipes use the temperature in the junction upstream. In AFT Arrow, however, isothermal flow is only realistic in pipes in which the velocity is very low, or when the pipes are very long. This implies that the heat transfer occurs in sufficient quantities to maintain the gas temperature close to the ambient temperature.
Adiabatic: The adiabatic heat transfer model assumes that there is perfect insulation and that there is no heat transfer in the pipe. In Arrow, this is a good approximation for short pipelines in which the gas has relatively little time to transfer heat.
Constant Heat Rate: This heat transfer model is straightforward: the heat added or removed from the pipe is fixed at the specified temperature.
Constant Heat Flux: This model allows users to specify a constant heat flux. It’s useful where the temperature difference between the fluid and the ambient environment is extremely large or in cases where a large radiant heat flux exists.
Convective Heat Transfer: Now let’s delve into one of the most common types of heat transfer modeled in AFT software: convective heat transfer. The window in Figure 1 shows the Pipes Properties window when convective heat transfer in a pipe is being modeled. Notice that an ambient temperature is required, as well as information regarding conductivity in the pipe, the thickness of the pipe, the heat transfer area, and the convection coefficient for the external environment.

The equation to calculate convective heat transfer is shown in Equation 1.

When modeling convective heat transfer, users can model up to six levels of thermal resistance including the fluid and the external ambient temperature. Three of these sources of resistance that are always present when modeling convective heat transfer include: the resistance from the fluid itself, the pipe wall, and the external environment. Optionally, users can model up to 3 layers of insulation with any combination of internal and external insulation.
Fascinatingly, the resistance to heat transfer behaves similarly to the resistance in electrical circuits. This means that the total thermal resistance summing any resistances in series and using the equation in Equation 2 to calculate the resistance for resistances in parallel.
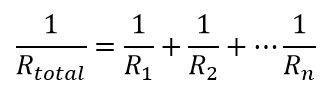
Equation 3 gives the total rate of heat transfer through a network.
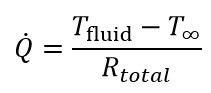
The calculations for the resistance to heat transfer due to conduction and convection are discussed below in the relevant sections. Note that the total resistance can be acquired by simply summing the individual resistances as shown in Equation 4.
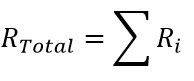
The fluid internal resistance is due to convection in the pipe. By default, the Gnielinski correlation is used to quantify the convection coefficient. The Dittus-Boelter correlation can be used if preferred by selecting it from the dropdown box. The resistance due to convection is shown in Equation 5.

The resistance due to conduction in the pipe wall and any specified insulation can be either radial (as in a pipe) or linear (such as in a plane wall). In pipes, the heat flow is not linear, but instead it is in the radial direction outwards from or inwards towards the pipe centerline. The thermal resistance due to conduction through a pipe wall is given by Equation 6.

The external resistance is based on a constant convection coefficient specified by the user, and a surface area obtained from adding up the thicknesses of the pipe and the insulation layers that are added to the pipe internal diameter.
Each resistance also allows the input of a multiplier on the calculated heat transfer area to account for things such as fins or other non-uniform geometries.
Let’s take a look at how AFT Fathom models heat transfer in pipes with the convective heat transfer model. The system in Figure 2 is flowing refrigerant that enters at -50°F, and the two heat exchangers control the discharge temperature to 70°F.
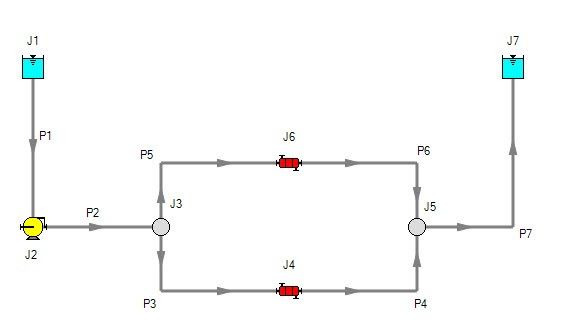
The Pipe Properties window shown in Figure 3 shows the heat transfer input parameters for this example including the ambient temperature and the heat transfer coefficients. Note in this window that only certain heat transfer information is required according to the type of resistance. For example, when heat transfer via conduction is occurring (such as in the pipe wall and the layer of insulation), the coefficient for thermal conductivity is required. However, because no convection occurs in those layers of resistance, the convection coefficient does not accept any input.
When we run this model, Fathom gives the output with the Heat Transfer as shown in Figure 4. Note that a Heat Transfer tab appears in the Output and the icon highlighted in red in this figure allows users to display a Results Diagram.
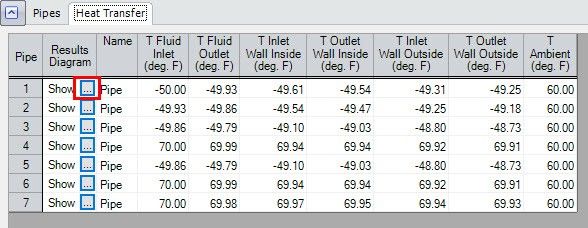
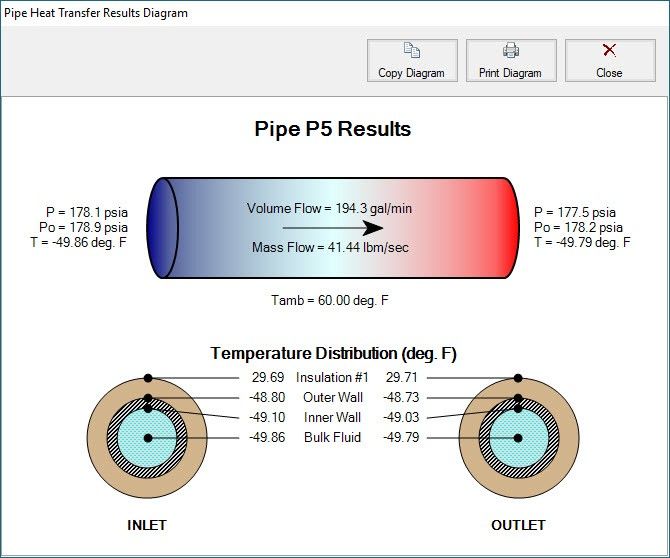
Clicking on this results diagram icon for Pipe P5 displays the image shown in Figure 5, in which the temperatures at different radial locations, as well as the pipe inlet and outlet, are displayed.
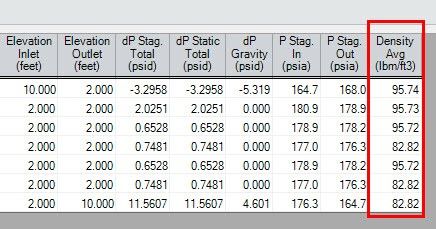
For one last note about heat transfer in pipes, return to the Output window and ensure that the Density Avg. parameter is being displayed in the Output. See Figure 6 to see it displayed for the model discussed in this blog. Remember that, for incompressible flow (AFT Fathom), density is assumed to be constant. However, when heat transfer is introduced into a model, the density of the fluid will change. In Fathom, this change in density is handled by sectioning each pipe into “thermal sections” and taking an average density. Note that the change in density is handled differently in AFT Arrow because Arrow calculates models the density at every pipe section, as opposed to averaging the density.
The ability to model heat transfer in AFT Fathom and AFT Arrow provides enormous advantage to many users of this software. With this ability, engineers can determine the heat lost or gained in their systems through pipes, pumps, and heat exchangers. Knowing this information can provide engineers the ability to determine if and how much insulation is needed, as well as give valuable information about the heat exchangers a system might need. For additional information about modeling heat transfer in heat exchangers, check out Abby’s blog.



Comments