AFT Blog
How does AFT Impulse model transient cavitation
The term transient cavitation is thrown around frequently when talking about the effects that transient events have on piping systems. It is widely and correctly understood to be something that can be harmful to pipes and pipe system components, but how to predict and calculate transient cavitation is not something that is as equally understood. In this blog, we will dive into what transient cavitation is, the two transient cavitation models that AFT Impulse offers, the differences between the two, and which one you should use in your model.
What is transient cavitation?
Cavitation is a phenomenon that can occur for any liquid when the static pressure is less than the vapor (or saturation) pressure. We are familiar with cavitation in our everyday lives – for instance, boiling a pot of water. As heat is applied to the pot of water, the temperature of the water increases. The increasing temperature raises the vapor pressure of the water. When the vapor pressure of the water reaches the atmospheric pressure, the water begins to boil.
The relationship between atmospheric pressure and vapor pressure is why water boils at a lower temperature when at a higher elevation where the atmospheric pressure is lower. The temperature does not have to get as high for the vapor pressure to equal atmospheric pressure. At sea level, water will boil at 212 deg. F (100 deg. C) but at AFT's offices in Colorado Springs, at an elevation of 6,000 feet (1,830 meters), water will boil at 200 deg. F (93 deg. C).
Conversely, instead of raising the temperature of water to bring it to boiling, the pressure can be lowered to get the same effect. Imagine if you are at sea level and you have a pot of water at 205 deg. F (96 deg. C), the water will be hot, but it will not be boiling. If you keep water at that constant temperature and then start driving up a mountain to get to higher elevation, thus lowering the pressure, at some point the water will begin to boil – and the temperature never changed. By the time you get to Colorado Springs, all the water will be completely vaporized. This change in pressure relationship more closely resembles cavitation when it occurs in a piping system.
In a piping system, a transient event such as a pump trip or valve closure can trigger high- and low-pressure waves to propagate through the system. If one of the low-pressure waves causes the static pressure of the fluid at a particular point to fall below the vapor pressure of the fluid, then the fluid will begin to boil, or cavitate, at that point. However, unlike a pot of water that just allows to vapor to escape freely, there is nowhere for the vapor to escape to. Consequently, when the pressure increases again, the trapped vapor cavity rapidly collapses. This causes significant pressure spikes that can damage pipes and components. Thus, it is important to model these transient effects in order to understand if and where cavitation occurs to avoid costly damage to equipment.
How does AFT Impulse model vapor volumes?
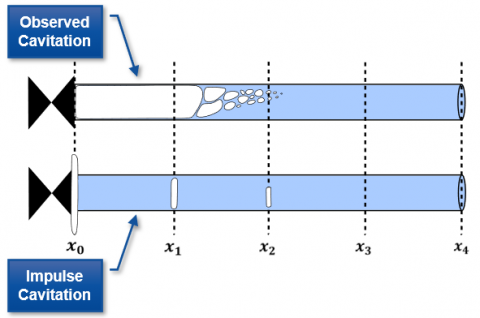
In order to perform the complex calculations of a transient system, AFT Impulse splits a pipe into multiple computing sections. The endpoints of each section is a station. AFT Impulse accounts for cavitation by modeling vapor formation only at these computation stations, x0, x1, x2, etc in Figure 1. AFT Impulse also assumes that the pipe remains liquid-full, and the vapor stays fixed at the station and cannot travel through the pipe.
For example, observed transient cavitation (referred to hereafter as simply "cavitation") in a pipe will take place over some volume of the pipe, displacing some of the volume that would otherwise be full of liquid. However, AFT Impulse models cavitation by assuming that cavitation is occurring at the pipe stations, as shown in Figure 1, in order to calculate the effects of cavitation while adhering to the engineering assumptions as much as possible.
There are two cavitation models that AFT Impulse can use in its solver to calculate when and where cavitation is occurring in a system: the Discrete Vapor Cavity Model and the Discrete Gas Cavity Model.
What is the Discrete Vapor Cavity Model (DVCM)?
The Discrete Vapor Cavity Model, or DVCM, is the default model in AFT Impulse. This model uses a binary assumption for cavitation: there is either absolutely no cavitation at a station or there is. Any station that has a static pressure at vapor pressure of the liquid is cavitating. There is no vapor or gas in the liquid at any static pressure greater than the vapor pressure, regardless of how close the static pressure is to the vapor pressure.
When cavitation is occurring in AFT Impulse, the vapor cavities are considered pure vapor at the vapor pressure itself and the solver uses that pressure as a new boundary condition at that point. In other words, AFT Impulse acts as if there is a fixed pressure equal to the vapor pressure at the station that is cavitating. With DVCM, pressure waves cannot travel across cavitating pipe sections making the pipe sections upstream and downstream of the cavitating section completely isolated from each other. A pressure wave will be reflected by the cavitation occurring at a station. This cavitation model is relatively less intensive, making it the default model for AFT Impulse.
What is the Discrete Gas Cavity Model (DGCM)?
The Discrete Gas Cavity Model, or DGCM, is a more advanced cavitation model. This model considers that vapor could be forming when the static pressure of the liquid is close to, but not yet at, vapor pressure. After all, liquid flow generally is not pure liquid as there is some amount of dissolved gas in most liquids. As the static pressure falls, the dissolved gas expands and comes out of the liquid to form bubbles. DGCM attempts to capture the gas formation prior to full vaporization.
Unlike DVCM, where pressure waves are reflected due to cavitation, the gas bubbles calculated in DGCM will have an effect of wavespeed. However, in order to maintain AFT Impulse's liquid-full assumption, DGCM coalesces the gas into a discrete volume at the computation station, just like DVCM.
This solution allows the wavespeed to remain fixed yet still allow pressure waves to propagate through the cavitating section. Similar to DVCM, once the static pressure of the liquid falls below the vapor pressure, AFT Impulse will effectively treat the station as a fixed pressure boundary condition, yet DGCM will still allow pressure waves to move through it.
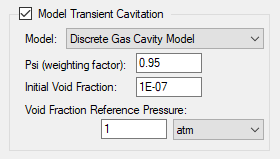
DGCM has three input parameters associated with it. The default values are typically sufficient for the vast majority of models and should not be changed without first discussing it with AFT Support. These parameters, shown in Figure 2, are:
- Psi (weighting factor) – used to weight vapor volume integration and should not be changed
- Initial Void Fraction – determines the initial volume fraction of the fluid that is free gas
- Void Fraction Reference Pressure – used with the initial void fraction value to se the initial free gas mass
What are the differences between DVCM and DGCM?
There are two major differences between DVCM and DGCM.
First, DVCM will not model any cavitation until the vapor pressure is reached while DGCM will model gas expansion as the system approaches the vapor pressure. Furthermore, DVCM will calculate cavitation as a step-change: as soon as the static pressure is calculated to be at vapor pressure then cavitation is occurring. The vapor pressure is then used as a fixed pressure at the point of cavitation. DGCM will calculate gas expansion and incorporate its effects in the calculations prior to actual cavitation occurring but will still effectively treat the cavitating station as a fixed pressure boundary condition once the vapor pressure is reached.
The impact that these differences have can be significant. With DVCM, vapor formation begins instantaneously when the static pressure falls below the vapor pressure and likewise the vapor collapses instantly once the static pressure rises again. This rapid vapor collapse can create artificial pressure waves in the system, meaning these waves exists in the numerical computation only and not in an actual system. These artificial waves manifest as numerical noise in the system. Modeling free gas expansion with DGCM can better capture real system behavior by eliminating this source of noise.
Second, DVCM does not allow any waves to cross a vapor volume while DGCM merely modulates those waves. As stated previously, when any vapor is present, AFT Impulse forces a pressure boundary condition at the cavitating station. DVCM prevents waves from traveling through the pressure boundary and instead reflects the waves. Alternatively, DGCM couples pressure and vapor volume to modulate pressure waves as they travel through the cavitating station. Because a gas cavity can have a variable pressure, a pressure wave slows as it travels through the cavitating section. Therefore, the pressure wave is both reflected and transmitted at the cavitating section.
The impact that these differences have can also be significant. DVCM can create noise as pressure waves from instantly collapsing vapor cavities create new vapor cavities at other stations, which likewise collapse and create more waves, which repeats the process. This cause-and-effect is known as pinging and is a purely computational behavior. DGCM better captures the behavior of a real system where waves will be partially transmitted and partially reflected through cavitating areas without pinging.
Which model should I use?
Systems vary greatly in the amount of cavitation that may occur during transient events. In systems with brief or no cavitation, DVCM is recommended because it is significantly less computationally intensive and can still provide highly accurate results. When there is extensive cavitation or when DVCM shows noise or chattering behavior, DGCM should be used.
As with most modeling alternatives, it is always a good idea to run scenarios with each cavitation model. If the two models agree, a high confidence can be assigned to the results. If DGCM shows a similar response to DVCM, but with less noise, place more confidence in the DGCM results. In the end, interpreting cavitation results can be difficult. Experience comes with time and practice.



Comments