AFT Blog
Analyzing Transients Faster - a Hacker's Guide to Pipe Sectioning
Over the past few months, I've gotten to help Impulse users from around the world with their models. One of the most common problems I run into while helping them is runtime. A good rule of thumb I try to use is that most Impulse models should take less than 10 minutes to run, and none should take more than a half hour to run. Longer runtimes mean the results can be more difficult to work with, and makes the analysis itself time-intensive as each change to the model requires the user to wait through the whole runtime before the results of that change can be understood.
Bringing a model from a 6+ hour runtime to less than 30 minutes can sound like a daunting challenge to even the most experienced Impulse user. Luckily, doing so is easier than it might seem. This blog will help you better understand what affects runtimes, and how to optimize your model for both rapid transient analysis and high accuracy.
How are pipes sectioned in Impulse?
To understand how to best set up your model for optimized runtime, it's important to understand how pipes are sectioned. Impulse sections pipes such that the pressure waves traveling through the model will travel exactly the length of one pipe section each timestep. To accomplish this, Impulse first determines the length of each pipe section and the wavespeed for each pipe.
Determining the length of each pipe section is the easier of these two tasks. In the simplest cases, Impulse uses the length of the controlling pipe (usually the shortest pipe) as the section length for the rest of the model. For more complicated cases, the controlling pipe might have to be broken into two or more pieces. The section length in that pipe is then used as the section length throughout the model.
Determining the wavespeed for each pipe is slightly more difficult. When pipes are defined in the model, wavespeeds for each pipe are calculated based on the pipe diameter, wall thickness, and pipe material, along with the bulk modulus of the fluid in the pipe. During sectioning, after the model's time step is determined, each calculated wavespeed is adjusted so the pressure wave takes exactly one timestep to travel the length of each pipe section in the model.
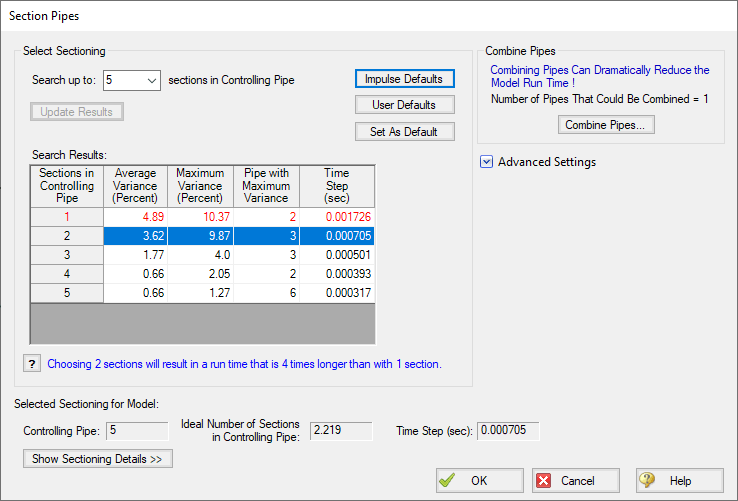
To minimize error in this process, Impulse also constrains the system to keep all wavespeeds within 10% of the values initially calculated. This limit can be changed by the user in the Section Pipes window, but the default limit of 10% variance sufficiently minimizes error in most models.
With these three steps, sectioning in Impulse works as follow:
- The software determines which pipe is the controlling pipe, and uses it as the section length in the rest of the model.
- Adjusted section lengths and wavespeeds are determined, checked against the original wavespeeds, and a variance is calculated for each pipe.
- This process is then repeated, breaking the controlling pipe into two, three, four, and five sections.
- Once all sectioning options have been determined, Impulse will pick the option with the fewest pipe segments that also meets the maximum variance limit.
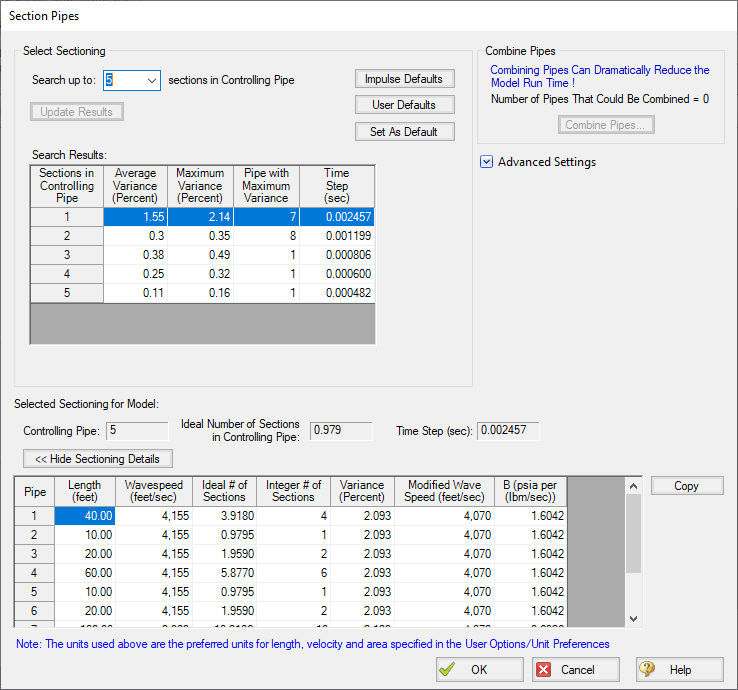
The details of this process can be seen in the Section Pipes window, as pointed out in Figure 1 below. We'll look more at these results later, with an example.
How can I optimally section a pipe network?
Now that we have a good understanding of how pipe sectioning works in Impulse, let's look at how to use it to our advantage and minimize runtime. To do this, there's two important factors to consider: the difference between the longest and shortest pipes in your model, and how individual pipe lengths compare to each other.
The first factor is relatively easy to understand. If the controlling pipe in your model is 6 in. long while the longest is 1000 ft., your longest pipe will have at least 2000 sections in it. As the number of pipe sections in your model decreases, so too does the runtime. Even a simple action like doubling the length of that controlling pipe from 6 in. to 1ft. would halve the number of sections in the model, substantially shortening runtime.
The second factor is slightly more abstract. Since Impulse has to keep wavespeed variance in each pipe below 10%, it can often be necessary to break the controlling pipe into two or more sections. The required number of calculations is a proportional to the square of the number of sections, meaning that keeping the lengths of shorter pipes as multiples of the controlling pipe's will dramatically reduce runtime.
With these two modeling strategies in mind, let's look at an example to see how much more efficient we can make Impulse.
Let's look at an example
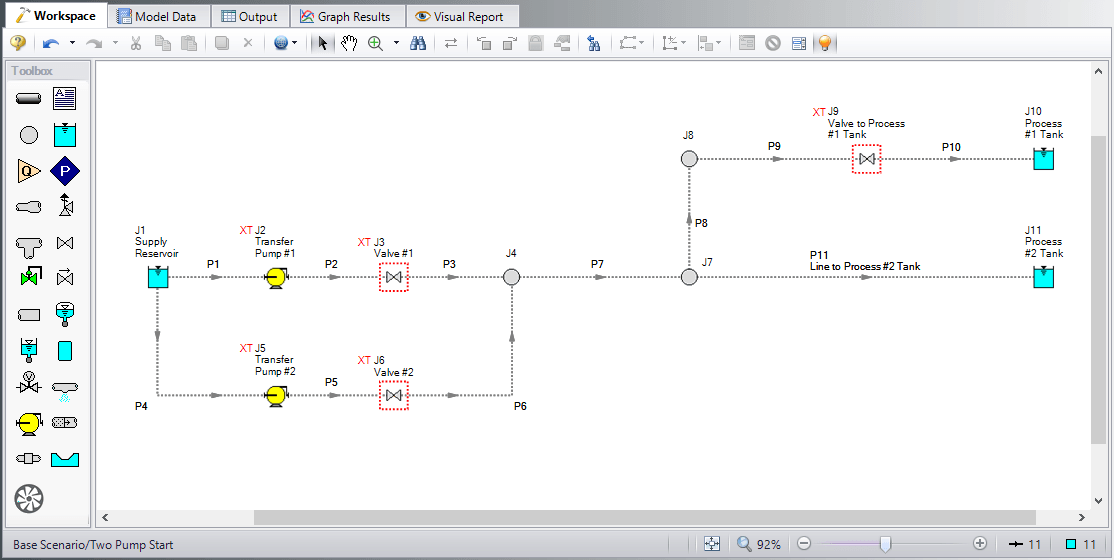
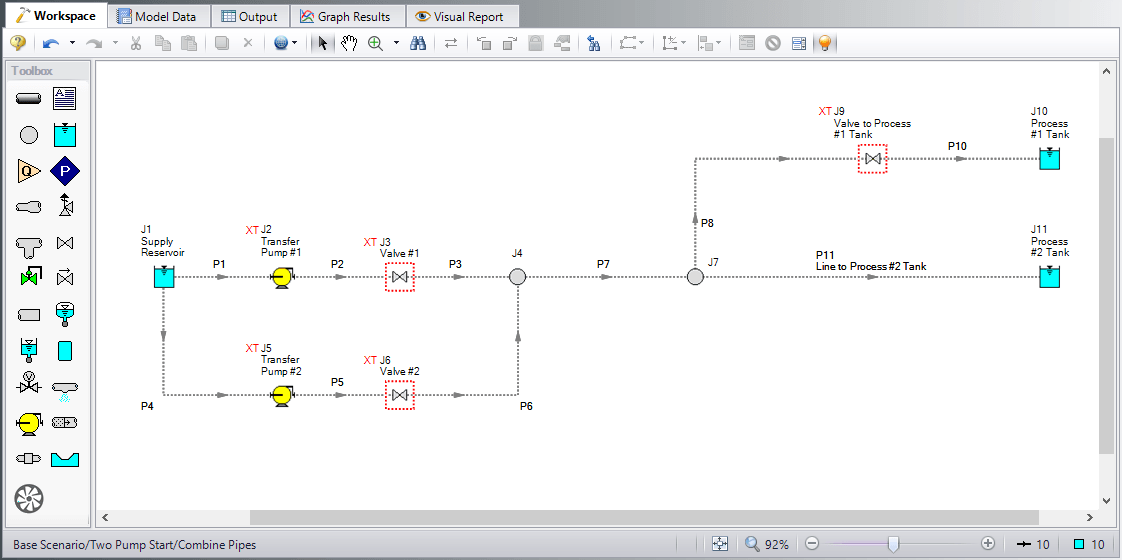
For this example, we'll use the system shown in Figure 2 below. It's a relatively simple system, based on the Pump Startup with Event Transients example installed with Impulse. Compared to the Pump Startup example, the only inputs that have changed are the pipe lengths, shown below in Table 1.
Looking through the model data, you can see that not only is there a wide range of pipe lengths (6.5 – 5200 feet), but the pipe lengths are all rather different.
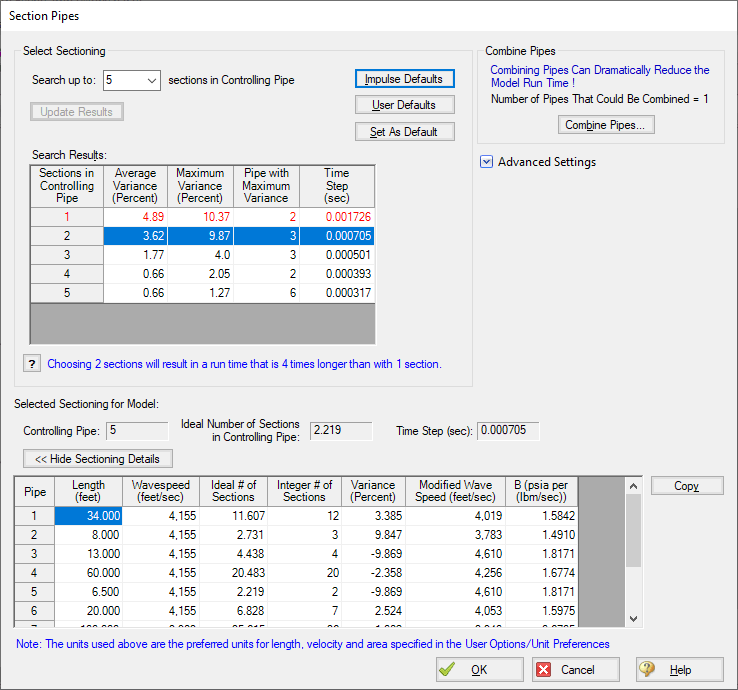
Examining the sectioning in this model (shown in Figure 3 below), the controlling pipe (P5), must be broken into 2 sections for the system to stay under the maximum 10% variance. With this sectioning, the longest pipe, P11, has 1,802 sections in it.
Running the model, we see a total run time of 3 minutes, 20.57 seconds. Relative to other Impulse models, this run time is rather short. However, for a system with only 11 pipes and 10 seconds of simulation time, this is a long run time.
Let's look at how we can easily reduce this model's run time. First, we'll use the 'Combine Pipes' feature shown in the Section Pipes window. This feature has been discussed in several other blog posts by AFT team members on combining pipes in general and while using resistance curves. The resulting system and pipe lengths are shown below in Figure 4 and Table 2.
In this model, combining pipes has not had a substantial impact on the sectioning or runtime. After combining pipes P8 and P9, our sectioning results have stayed the same, with two sections needed for the controlling pipe, and 1,802 segments in the longest pipe, P11. The runtime for the model stayed effectively constant, at 3 minutes, 17.54 seconds.
However, many models will see dramatically reduced runtimes just from combining pipes. I always encourage users to combine their pipes, as they can see run times orders of magnitude shorter from just that simple action.
Our system can still be modeled more efficiently, using the methods we discussed. Let's first set our pipe lengths to be integer lengths. Table 3, below, shows the new pipe lengths in our model. In this example, pipe P5 was rounded from 6.5 to 8 ft, to be equal in length to pipe P2.
With this system, we see that the number of sections in the controlling pipe (P5) still needs to be 2. However, with a run time of 1 minute, 32.02 seconds, we can see that this step is still effective in helping reduce run time in this system. In many larger systems, this step alone can result in far more substantial run-time reductions.
We can still improve the run time in this system further, so let's go ahead and set our pipe lengths to be multiples of 10 feet. Not only will this allow the controlling pipe to have a single section, but it will also limit the number of sections in our longest pipe, P11. Table 4 below shows our new pipe lengths, and Figure 4 shows the sectioning results for this new system.
From these sectioning results, we can see that the controlling pipe now has a single section. The number of sections in P11 has been reduced to only 517 sections, and the model now has a run time of 15.59 seconds. Compared to our initial run time of 3 minutes, 20.57 seconds, this model runs almost 13 times faster.
We've now seen how powerful proper sectioning can be, even on this relatively simple model. In more complex systems, this approach can reduce run time from a whole work-day (or longer) down to a handful of minutes.
However, we now have a different model than before. Not only have we reduced the number of pipes in the model, but we've changed the lengths too. This model no longer matches the geometry of our real system. Let's take a look at how our accuracy has been affected.
How does this impact accuracy?
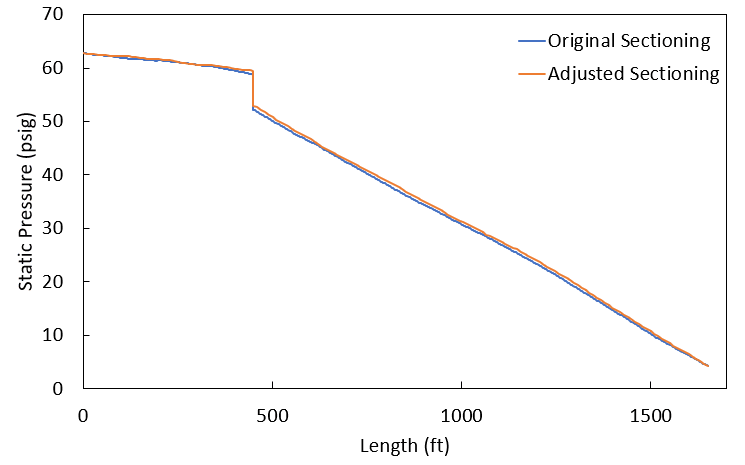
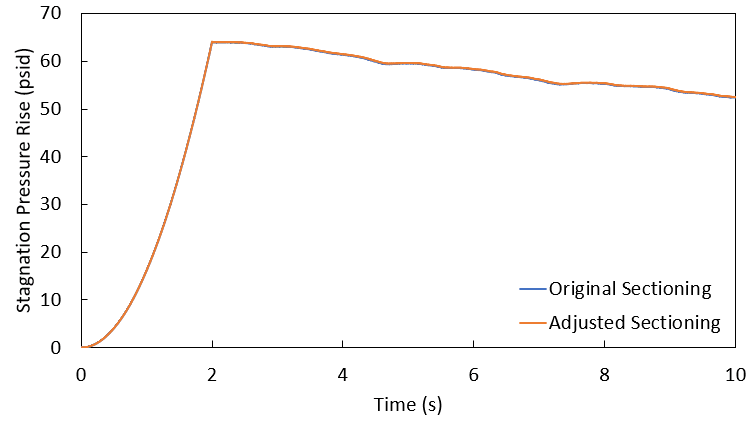
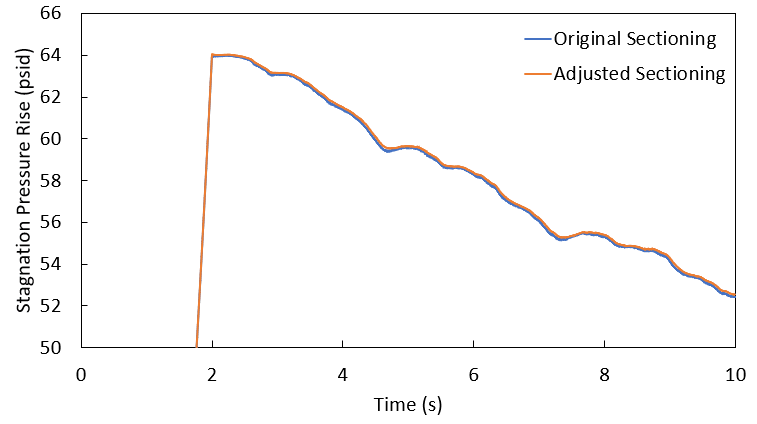
For this analysis, we're going to look at the pressure profile along the branch to the Process #1 Tank, and the Pressure Rise vs. Time curve for our Transfer Pump #1. Figures 5-7 below help make this comparison. In these figures, the blue line shows data from the sectioning in the original model, while the orange line shows data from our final scenario, with pipe lengths in increments of 10 ft.
As we compare these results, it is easily seen that the two scenarios – with vastly different sectioning and even a different number of pipes – effectively yield the same results. In fact, in the full graph of pressure rise at the Transfer Pump #1, it's almost impossible to tell there are two lines plotted, and it's only once the scale on the graph is zoomed in that we can begin to distinguish the curves.
Taking the original sectioning results as our benchmark for accuracy, these graphs show us that adjusting the lengths of pipes in this model causes the pressures to vary by no more than 1 or 2 psi. Especially when accounting for the inherent uncertainties in any transient fluid analysis, the differences in our model are effectively negligible. Impulse is predicting the same results at the same times in our two scenarios regardless of how we have sectioned this model, and the same holds true for the other sectioning configurations we looked at.
This is, of course, a highly simplified model, and most users have models that are vastly more complicated. They might see slightly more discrepancies in results between their original systems and the systems modified using these approaches. However, as we've shown, those discrepancies are usually minor, and almost always within the uncertainties inherent to using AFT Impulse.
With this discussion, we now have a solid understanding of how pipe sectioning works in Impulse, and several approaches to optimize run time. By limiting the number of pipes in a model, and working to define pipe geometry such that the number of pipe segments is minimized, we can perform transient analysis faster than ever, without sacrificing accuracy.
It is important to note that sectioning can impact some uses of Impulse. When cavitation is present in the system, transient forces are being calculated, or the partially full pipe tool is being used, the approaches we've looked at today can affect a model's results. The pressure and flow results typically remain unaffected, but with cavitation for example, having longer sections means Impulse will report that pipes will have a lower percent vapor volume than with shorter sections.
For more information about pipe sectioning, or Impulse in general, check out the AFT Impulse Help files, found in the Help menu within the Impulse software, visit some of our other Impulse blog posts, or come visit us at our office in Colorado Springs, Colorado for our Impulse training seminars.



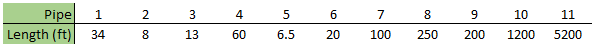
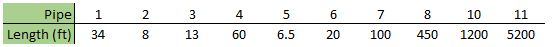
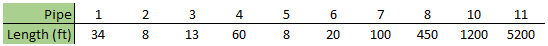
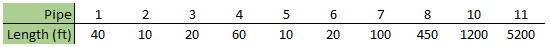
Comments