AFT Blog
Reference Pressure Needed: Where It Comes from and How to Address it
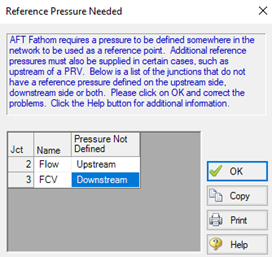
Many AFT users have come across the message that a reference pressure is needed when attempting to run a model but do not often know how to handle it. Why is it showing up? What can they do to fix the issue? Before going too far, it is important to understand the problem is a limitation of physics and math, not of AFT software. We will work through this concept from the perspective of AFT Fathom (incompressible flow).
[This discussion gives another view on the same topic found in Fathom's Help Guide: Role of Pressure Junctions and How They Work.]
Model defined by two flow rates:
The simplest way to demonstrate the issue is when two junctions in series are defined by flow rates, like below. We have 1000gpm moving through a section of pipe. Trying to run this model will trigger a reference pressure error.
Think simply that flow arises from a pressure difference, high to low. Based on the pipe and fluid information (length, diameter, friction, and fluid density) we can determine the required pressure difference from Bernoulli's equation, including frictional loss of course.
The last right-hand term represents frictional loss. For incompressible flow in a straight pipe, ignoring elevation changes, we can simplify to:
We have all the terms on the right-side known: friction factor, length, diameter, fluid density, cross sectional area, and flow rate. Based on this specific model, there is a pressure loss of 10psi. However, fundamentals of algebra tell us the equation is still not solvable. There are two unknowns left, P1 and P2, and one equation. We need one of those pressures defined as a reference.
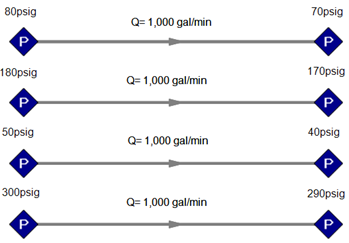
There are an infinite number of pressures that give a difference of 10psi. Knowing only a "delta" is not enough. Below is output from four Fathom models, showing how each pipe results in the same flow rate because each model has a 10psi difference. Getting 1000gpm is not unique.
So, Fathom will report a reference pressure issue in a model only defined with flow rates because there is no unique solution. How is defining the same flow rate twice helpful anyway? Fathom needs something to solve for with 0 degrees of freedom.
Instead of defining two flow rate boundaries, I should define one flow rate and one pressure boundary, or define two pressure boundaries.
An alternative to Assigned Pressure junctions are Reservoir junctions. They both define pressures, just in different ways. Assigned Pressures ask you if you are defining stagnation or static pressure - see this video for more info on the difference.
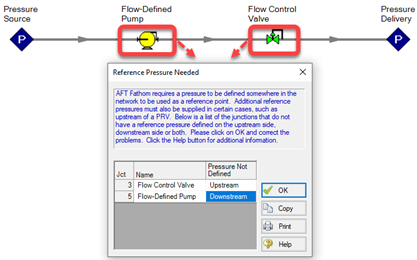
Flow-defined pump and FCV in series:
It is not as easy to see the issue at first glance. The model does, indeed, have pressure boundaries defined; however, this problem is just like the issue above where two components are defined by flow rates.
When the pump and FCV are forced to meet a certain flow rate, they vary their pressure rise/drop to whatever is necessary to meet their setpoint. The points after the pump are "cutoff" from any upstream pressure information because the head rise can be whatever is needed. It is not limited. The discharge pressure is determined only from the downstream pressure boundary, the pump-specified flow rate, and solving Bernoulli's in between.
The FCV is similar in that it will drop the pressure to whatever is needed to get its flow rate based on the downstream pressure. Anything upstream of the FCV is "cutoff" from the downstream pressure boundary. It can drop the pressure from any upstream pressure. It is not limited.
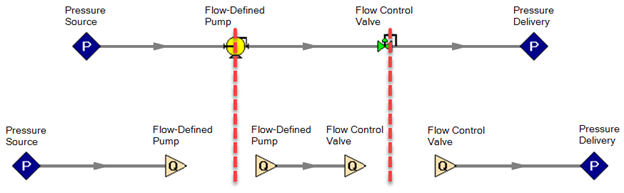
The problem is that the FCV does not know the upstream pressure because the pump does not know its discharge pressure. The pump does not know its discharge pressure because the FCV does not know its loss and subsequent upstream pressure. There is no solution to the problem. You can think of any forced setpoint as an internal boundary condition. The models below effectively show the same system.
The solution between the pressure source and pump, and the points between the FCV and pressure delivery can be found easily. However, the solution in between the two cannot.
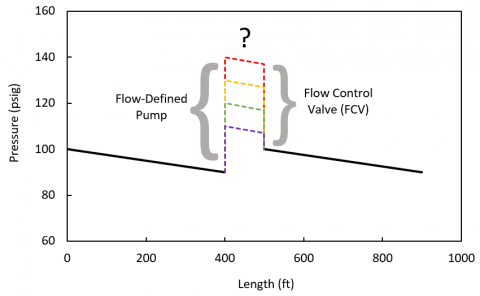
The profile graph below may help clarify. It depicts how the pump can increase pressure to any point because the FCV can drop the pressure starting from any point. The black lines at the ends are known pressure profiles, but the colored lines in the middle are unknown. There are again an infinite number of solutions.
There are several resolutions users can take in this example, including:
- Entering a pump curve (without a flow-controlled VFD), so that there is a fixed pressure rise with each flow rate. The FCV then tells Fathom what the system flow is.
- Defining a "sizing" pump based on a pressure rise instead of flow.
- Defining the FCV as a constant pressure drop valve or a pressure sustaining valve.
- Many more…
Unfortunately, there is no straightforward answer for how the user should change the model inputs. It depends on the system and what assumptions can be made. The bottom line is the user must "open up" the middle part of the model for it to read pressure information from the boundaries.
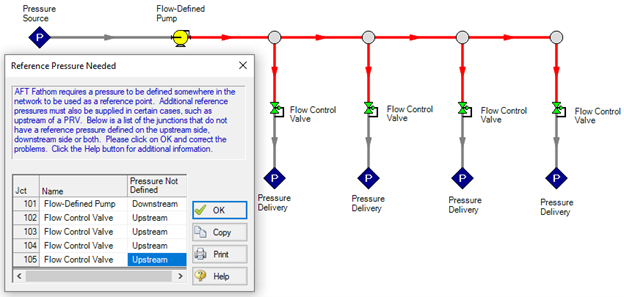
Branching (parallel) pipe systems:
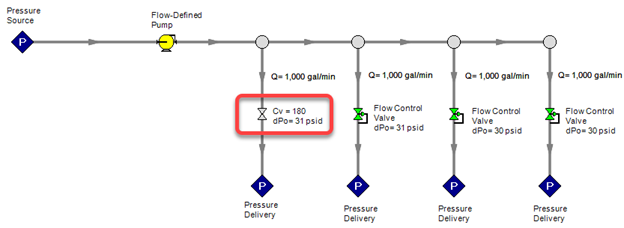
The message tells you exactly where the problems are: downstream of the pump and upstream of the control valves. We need to find a way for those parts to see a reference pressure from the boundaries. In this case, we can change out one of the control valves to a regular valve with an assumed Cv (or loss factor). Because the loss is fixed, unlike the loss of control valves which dynamically update depending on what's needed, there will be a known pressure upstream of the valve which can be "seen" by the other parts. Just one valve change is enough to fix our problem.
Below is the model output from changing the valve to a fixed Cv (180 in this case). The flow distribution will still be even because Fathom knows how to balance mass. If 4 out of the 5 junctions have defined flow, it will automatically find the fifth flow. Because Fathom finds the flow rate in that branch, it knows the associated loss and upstream pressure. Now there is a reference pressure seen inside the middle part of the model that can be read throughout. There are now 0 degrees of freedom for all the mass and momentum balances.
Your models may be much larger than the examples shown here, but hopefully you can take what you learned and apply it to your systems when that formidable "reference pressure needed" error pops up!
If you want to take an even deeper dive into the topic, check out our detailed discussion in Fathom's Help Guide: Role of Pressure Junctions – Detailed Discussion.



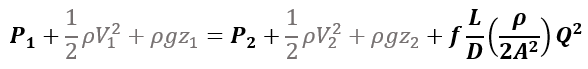
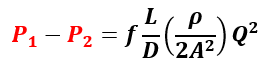
Comments