AFT Blog
Line Packing: Recovering the Irrecoverable
Have you ever been working on an interesting project where you get into the zone by picking up so much momentum in the work you are doing? But then, all of a sudden you hit a brick wall in your progress and cannot help but feel the pain of all that momentum coming to a screeching halt? You are not alone, in fact, fluids experience something very similar.
When fluids are traveling through a pipe and suddenly coming to a halt, by closing a valve for example, there is a pressure spike at the end of the pipe because of the transfer of energy from velocity to pressure. This event is called waterhammer, named after the sound that can be heard as the fluid comes to a stop. A key point of interest for engineers designing a system where a valve could shut and the fluid comes to a stop is what the pressure spike could be and if it exceeds the maximum allowable pressure in their pipeline. Many engineers in this situation are familiar with a handy equation to calculate this pressure spike, called the Joukowsky equation.
Although the Joukowsky equation is an easy and reliable way to determine instantaneous pressure rise that can occur by quickly closing a valve, there is more that is occurring in the system than what this equation is considering. In this blog, we will explore the limitations of the Joukowsky equation, a phenomenon called Line Packing, how irrecoverable losses are actually recoverable, a better way to predict maximum pressure rise, and how AFT Impulse can do it all.
The Joukowsky Equation
The Joukowsky equation is an easy calculation to perform, any freshman engineering student should be able to use it and understand what it is calculating.
The pressure rise of a fluid in a pipeline is the product of the density, the wavespeed (a function of the bulk modulus, or how resistant a fluid is to compression, and the density), and the change in velocity of that fluid. It calculates the pressure increase that can occur when there is a sudden change in velocity. This pressure increase is added to the steady state pressure at the end of a pipe to see what the pressure spike will be if a valve is closed quickly at the end of that pipe.
To visualize this, imagine one of those test cars that is sped up to a high speed then is run into a wall to see how strong the car is. There is a lot of energy released as the speed of the car instantaneously changes from very high to a dead stop. For a fluid, the primary destination for this energy is in the form of pressure. When the fluid comes to a stop, the pressure increases, and the Joukowsky equation helps relate that energy change.
The Joukowsky equation has many names, it is known as the "maximum theoretical waterhammer equation" and the "instantaneous waterhammer equation." It is also considered a conservative, rule-of-thumb equation to use to assess what the maximum pressure rise will be if the fluid in your system suddenly comes to a stop. Both the name and the intent are misleading: the Joukowsky equation is only part of the puzzle when trying to piece together what happens when fluids come to a stop.
Line Packing
As fluid moves through a pipe it is rubbing against the internal pipe wall. This friction against the pipe wall is slowly dropping the pressure across the length of the pipe. This pressure drop is even more pronounced when the fluid is traveling very quickly or when the fluid is very viscous or thick.
Now, instead of imagining a speeding test car running into a wall, make it a 5-mile-long freight train hitting that wall. The first few train cars come to a stop almost right after the wall is struck, but the caboose at the end of the train will not come a stop at the same time that the front train car comes to a stop. That caboose is going to keep moving down the track, along with many of the other cars, because of the large amount of momentum those train cars have. The information that the front of the train has come to a stop is quickly, but not instantaneously, being transferred to the back of the train. The speed that this information is passed back the train is called the wavespeed, and until a traincar receives the notification to stop, it will keep moving at its original full speed. Once it comes to a stop, the momentum of that traincar will be converted to another form of energy.
Line packing is very similar. It is of high concern for engineers who are designing long pipelines that are measured in hundreds of miles because of the high amount of momentum that these lines are transferring. When a valve at the end of the long pipeline is closed, there will be an instantaneous pressure rise, just like the test car hitting the wall. However, there is still a long train of fluid that still needs to come to a stop, but the information to stop has not been passed all the way up the pipeline yet. The fluid in that line will continue to move down the pipeline, and "pack" the line. The Joukowsky equation is very helpful for determining the initial pressure rise, but how can we estimate what the pressure rise will be as the rest of the fluid comes to a stop?
When we think about it, where could that pressure be coming from that starts to show back up when the fluid comes to a halt? The same place where pressure was being lost to when the pipeline was at steady state: friction. If we look at how much pressure loss occurs due to friction across the entire pipeline, we get an idea of how much the pressure will rise as the fluid stops. Now if we add this friction recovery pressure rise to the instantaneous pressure rise from the Joukowsky equation, we get a conservative estimate of what the maximum pressure rise in the system will be. Then if we add this maximum pressure rise to the steady state pressure at the valve at the end of the pipeline, we get a good look at what the maximum possible pressure could be at this point after all the momentum all the way down the pipeline is transferred to pressure. This is captured in the following equation:
This may seem a bit odd, aren't friction losses irrecoverable? Well, yes and no. A pressure loss from an elevation gain can be recovered by an elevation drop, this is an example of a recoverable pressure loss. The same goes for a decrease in static pressure as a result of a velocity increase: that static pressure can be recovered when the velocity decreases back to its original value. But what about friction? Consider what the pressure in a line will be once a downstream valve has closed and all transients have steadied out. Assuming no elevation change, the pressure in the entire line will equal the upstream pressure because there is no flow. The conclusion that friction losses are irrecoverable assumes that the fluid will always be flowing. Thus, the "irrecoverable" losses that were originally due to friction are now recovered.
Although line packing is most pronounced in long pipelines, it should still be of concern for plant engineers who are designing lines with much smaller flowrates and diameters. It has been demonstrated on relatively short pipe systems that line packing can still contribute a significant pressure rise after the initial instantaneous pressure increase.
Can AFT Impulse simulate line packing?
So now I bet you are asking, "okay, this is a better estimate than just using the Joukowsky equation to estimate maximum pressure rise, but how can I model my system to see what it actually might be? Can AFT Impulse simulate line packing?" The answer is yes! Let us see it in action.
AFT Impulse and Line Packing in Action
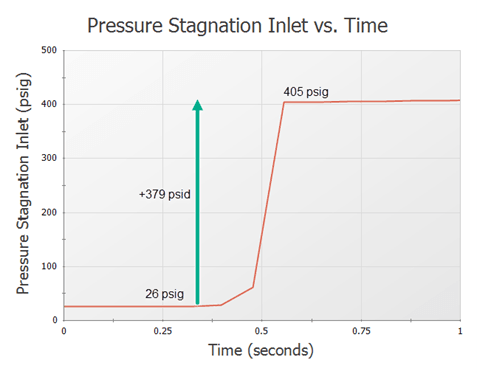
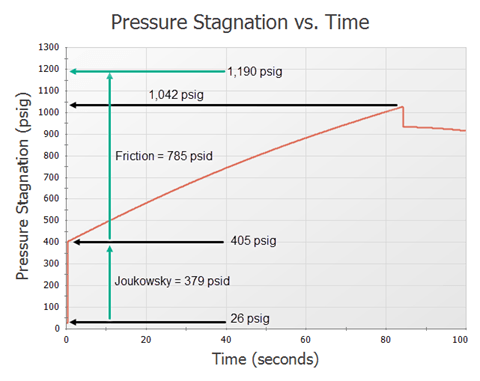
For this model, we have a 30-mile-long 20-inch diameter pipeline that is moving over a quarter million barrels per day of semi-light crude oil with an API gravity of 31.1 degrees or 870 kg/m3. At this flowrate and diameter, the fluid velocity is 2.6 meters per second. The pipe material is Steel – ANSI and the pipe support model is for a thick-walled pipe anchored upstream, which AFT Impulse uses to calculate the wavespeed: 1,152 meters per second. At the end of this long pipeline, there is a valve leading into a tank. If we set the valve to close nearly instantaneously, we can see the initial pressure spike when the velocity drops to zero, which should be approximately the pressure rise predicted by Joukowsky.
From the model results, we see a 379 psid instantaneous pressure increase at the inlet of the valve right after the valve shuts, exactly what the Joukowsky equation calculated! An unwise engineer without any knowledge of line packing will take one look at this and conclude that that the maximum possible pressure at the end of this pipe is 405 psig. But now that we have a knowledge of line packing, we know that this system warrants further investigation.
If we set the time duration to be long enough, we can watch the effects of line packing. There will be a steady pressure rise that occurs as the rest of the fluid comes to a stop and the friction pressure losses are recovered. Looking at the steady state model, friction pressure losses are equal to 785 psid.
When we compare our calculated maximum pressure rise of 1,164 psid (1,190 psig maximum pressure) to the AFT Impulse's predicted pressure rise of 1,016 psid (1,042 psig maximum pressure), we can see that although the Joukowsky plus recovered frictional loss calculation is a conservative one, it is still very handy at approximating the maximum pressure. As shown, AFT Impulse does model the pressure rise as a result of line packing.
Conclusion
Whether you are designing a cross-country pipeline or a short line in a small plant, line packing must be taken into consideration. Additionally, line pack is not the only phenomenon that can increase the maximum pressure in a pipeline. For more information on when the Joukowsky equation fails, check out this technical paper When the Joukowsky Equation Does Not Predict Maximum Water Hammer Pressures.
The calculations discussed here can help you quickly assess the impact of momentum on your system and AFT Impulse can help you keep your own momentum going by providing a way for you to model your system and see these impacts for yourself.



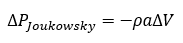
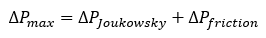

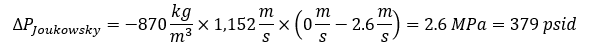
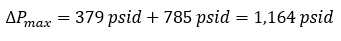
Comments