AFT Blog
A Story About Fluid Communication
Jack, Ryan, and Sally are piloting a small research vessel on a remote river. While distracted by news of the Mars 2020 Perseverance rover (successful landing!), their vessel crashes and begins capsizing. After their initial panic, they are dismayed to find the collision has taken out their communications equipment.
In some quick thinking, Jack finds a printed log of ships expected to be nearby. Fortunately, there is a marine zoology expedition about a mile downriver, and our crew just needs to get an SOS out to that ship.
Initially, Jack tries simply yelling for help. Unfortunately, this doesn't do much good - and the explanation why requires some fluid mechanics.
Any disturbance in a fluid will propagate an acoustic wave. This wave happens simply because molecules collide with each other and pass on the message, like an enormous game of Telephone. Individual molecules do not move very far - they just bump into their neighbors.
On a molecular scale these collisions happen incredibly quickly. The macroscopic speed at which the wave propagates is the speed of sound. You can see and hear it in the delay between a lightning strike and its thunder.
Air is highly compressible, and each molecule moves a lot when it is relaying Jack's message. This motion causes substantial dissipation - by the time the sound wave reaches the expedition ship, it is too weak to hear.
Key Lesson 1: Molecular interaction carries information through fluids.
Not to be deterred, Ryan suggests they send a message in a bottle downriver. They write their note and send it floating away, only to realize that it will take far too long to reach the expedition.
This is another message being carried by a fluid. In this case, the message itself is being physically transmitted. This is only possible if the fluid is moving, and its speed will match that of the bulk flow.
Particles suspended in a bulk flow carry information this way, which is often important. A change in flowrate, for example, can only be communicated throughout a system as fast as the flow velocity itself.
Key Lesson 2: Flowing fluids carry messages independent of the fluid's speed of sound.
The message in a bottle was a bad idea in retrospect. In the meantime, Sally discovered that the zoological expedition is studying dolphin communication. She frantically searches for a hammer and starts pounding out an SOS on the hull of their vessel. Her colleagues are bewildered, but she just saved the day.
Sally has sent the same kind of message that Jack did - an acoustic wave. The only difference is the medium - the water of the river. Sally knows that dolphins communicate via echolocation, and - if the expedition was listening for underwater communications - they will easily hear the SOS.
There is a simple but critical difference to Jack's acoustic wave - the water is much less compressible than the air. As the molecules are tightly packed together, they pass on the message much more quickly and with far less dissipation. Even very stiff materials like steel communicate information in the same way.
Key Lesson 3: The wave velocity and energy dissipation in a fluid depends heavily on its compressibility.
The expedition visually signaled they heard the SOS and are on their way. It's a race against time though, as the vessel is still sinking. One of two bilge pumps is broken, and the crew needs to know if the rate water is coming in will overwhelm the remaining pump.
The leak gets faster with higher fluid pressure. And the fluid pressure depends on the depth – let's explore why.
It is difficult and unnecessary for almost any application to analyze fluid at the molecular level. Instead, we break it up into small "blocks," or differential elements, each with mass and compressibility.
If we put one such block of fluid in a graduated cylinder, it will exert its weight on the table as pressure. If we add a second block on top of it a few things happen:
A) The top of the first block sees a pressure from the block above it
B) The table sees double the pressure
C) The bottom block gets compressed
We can calculate the pressure on the table with the total weight and cross-sectional area. The weight is simply the total mass times gravity, which we can find with an average density and dimensions. Combining these, we get a familiar equation for hydrostatic pressure.
Ryan did a quick calculation and found that the remaining bilge pump will be overwhelmed and requires immediate repair. He grabs his tools and goes to work.
As an aside, it is important to note that the rho used in the hydrostatic equation is an average. If, for example, we try to reverse calculate the height of the atmosphere from air pressure and density at sea level, we get a result that implies the cruising altitude of a 747 makes it a spaceship.
We've dramatically overestimated the average density and the effects of compression. On the other hand, liquids generally have very low compression even under extreme conditions. At the depths of the Mariana Trench (36,200 feet) there is a pressure of nearly 16,000 psi. Even at this tremendous pressure, the density of water increases less than 5%.
Key Lesson 5: High compressibility makes things complicated quickly, even for simple cases. For liquids we can neglect it in most calculations.
While fixing the pump, Ryan accidentally drops his wrench, and it is headed squarely for his foot.
While Ryan may not know it, this situation is going to help us explain some more details about the mechanics of fluid waves.
Just how much Ryan is going to regret his clumsiness depends on how high the wrench was dropped from. The mass of the wrench never changes, but how long it is acted upon by gravity determines its velocity (up to some terminal velocity). It is this velocity that is going to hurt. Certainly, if Jack had thrown the wrench in despair, the situation would be more dire (for Ryan's foot and the crew). Fortunately, our crew gets along a little better than that.
In the end, this will be a painful lesson in momentum. Newton's second law states that the rate of change in momentum is equal to the applied force. If the mass is constant, this is simply F=ma.
The acceleration that is going to be shortly transmuted to a scream is not acceleration due to gravity. It is instead the acceleration of the wrench as its fall is halted. This acceleration depends on how elastic the collision is, and the wrench is not very elastic, so let's hope Ryan remembered his steel-toed boots. The faster the wrench is brought to rest, the larger the force will be.
Key Lesson 6: The force on an object depends upon its change in momentum.
Ryan is certainly upset at his mistake, but he has nonetheless managed to repair the pump, and the water level is stabilized. It appears that the crew is no longer in crisis.
The falling wrench may not seem to be related to fluid mechanics, but fluid flow is in fact governed by the same physical laws. Instead of a falling wrench contacting an unexpecting toe, let's consider a column of falling water. We assume our column of water is falling uniformly with a constant diameter and without any air pockets forming within it. What happens when this column hits the ground?
First, consider the forces just before collision. There is a force from gravity, but the water is accelerating because of it. In effect, the water is in free-fall and weightless. The pressure at the bottom of the column isn't any higher than the pressure at the top.
What about immediately after collision? Just like the wrench, there will be a substantial pressure and force. And just like the wrench, we have momentum to thank.
Let's consider the bottom block of fluid, as we did before with the hydrostatic example. This block is traveling at some velocity but will shortly be stopped entirely. This change in velocity over some time is our acceleration. The mass of our block does not change.
The piece we are missing is how long it takes the block to stop. For this, we need to remember that information travels through the fluid in a molecular wave. Stopping the fluid is just like communicating with Sonar or yelling through the air in this respect.
At the exact instant of collision, the fluid is still moving downward. After an extremely short time, a few layers of molecules are halted, but most of the block is still moving unimpeded - the stoppage hasn't been communicated to that fluid yet.
Key Lesson 7: Momentum is critical to the force on a moving fluid, just like a solid object. For a fluid, however, analysis of wave mechanics is necessary.
Going back in time a bit, this molecular action is akin to the first moments after Sally hit the hull with the hammer. A wave passed extremely quickly through the steel of the vessel, and then slower (but still very fast) into the water. In Sally's case, the fluid was initially at rest, but the idea is the same.
Note: This equation is simply an application of conservation laws known as the Instantaneous Waterhammer Equation, or Joukowsky Equation. A true derivation is more involved, and the result is usually presented with a negative sign - it is important to keep tabs on the definition and sign of dV.
Key Lesson 8: The magnitude of a pressure change depends only on a local change in velocity. The water column could be 1 foot tall or 50 feet tall – if the initial velocity is the same, the pressure increase will be the same.
In Sally's case the change in velocity of the water is extremely small, and therefore the change in pressure is extremely small. Fortunately, our ears and listening equipment is remarkably sensitive. In Ryan's case (unfortunately), or in the case of a falling water column, the change in velocity is substantial, resulting in large pressures and forces.
After the wave completely passes through the first block, it simply continues to the next, repeating the process, and transmitting a pressure wave of essentially the same magnitude from block to block. The lower blocks get compressed, but for liquids this effect is negligible.
Key Lesson 9: The magnitude of the pressure wave is dissipated only by friction like effects. If there was no dissipation, it would continue at the same magnitude forever.
The molecular wave that Sally generated traveled from the sinking vessel to the expedition microphone layer by molecular layer. Unlike the Jack's yell in the compressible air, the dissipation in the liquid water was much lower and could easily travel the thousands of feet required. The physics behind the wave and its magnitude can be seen all around us in everyday life but aren't always easy to recognize. Fortunately, with some quick thinking and perseverance, a much worse outcome was averted.
This story was just a fun way to discuss some fundamentals of flow dynamics. But the wave action described here doesn't just impact fictional characters – these waves are propagated in your piping systems any time you change operational conditions – without exception! Sometimes the waves are negligible, but sometimes they can destroy systems.
The falling water column above is nearly exactly analogous to suddenly closing a valve against a moving flow. The faster the initial flow, or faster the closure, the larger the force you will see. Instantly (or effectively instantly) stopping the 10 ft/s flow of water in a typical 4" pipe will cause a pressure increase of over 500 psi.
Unfortunately, analyzing these effects in a piping system is much more difficult than applying the equation above. Fortunately, tools like AFT Impulse make this complex analysis a breeze.
Key Lesson 10: These effects happen in every fluid system. Dramatic pressure changes can easily occur during normal or emergency operational changes. Especially in liquid systems, relatively low dissipation means a high energy wave generated in one location can damage equipment a very long way away.



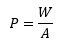
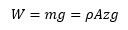
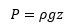
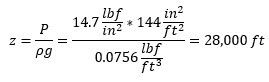
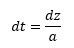
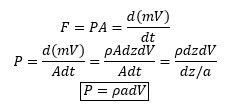
Comments