Superheated steam is often used in mechanical power applications, such as driving turbines. For heating or industrial processes, however, saturated steam is more efficient. Desuperheaters are used to lower the temperature of superheated steam, so that it can be more effectively used in industrial processes. A desuperheater lowers the temperature of the steam by injecting water.
Now, the question is, how can you model a desuperheater within AFT Arrow? AFT Arrow is a single-phase program for compressible flow, so it cannot model liquid water. Conveniently though, there is a feature built into the branch junction that can model a desuperheater.
You may have noticed that on the Optional tab of the Branch Properties window, there is a box for Flow Source or Sink. If you select this box, you will have the option to specify a source of flow into the system. This flow can have a defined enthalpy. To model a desuperheater, you can input the mass flow rate and enthalpy of your water stream. AFT Arrow will then perform the necessary mass and enthalpy balances.
Overall, when you define a branch in this way, you will see an increase in mass flow and a decrease in temperature at the branch. This is exactly what you would expect to see happen at a desuperheater.
Here is an example:
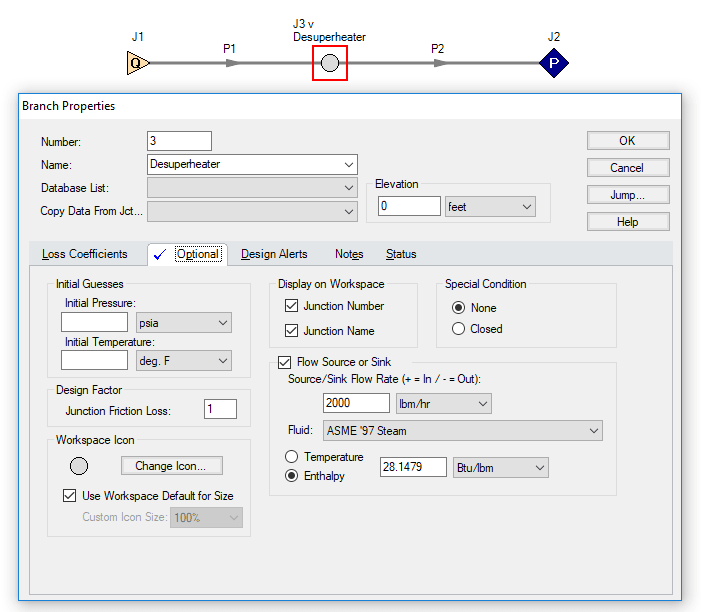
In this simple model, there is an assigned flow junction with 10,000 lbm/hr of ASME ’97 Steam at 1000 °F. The other boundary condition is an assigned pressure junction with 10 psig steam. The branch junction, as defined above, is representing a desuperheater that injects 2,000 lbm/hr of water with an enthalpy of 28.1479 Btu/lbm. This enthalpy was calculated using AFT SteamCalc for liquid water at 10 psig and 60 °F.
Now, what is the effect of the desuperheater on the system? The branch models the injection of the liquid water and as expected, the mass flow increase from 10,000 lbm/hr to 12,000 lbm/hr. The temperature drops from about 1000 °F to 496 °F, as shown below.
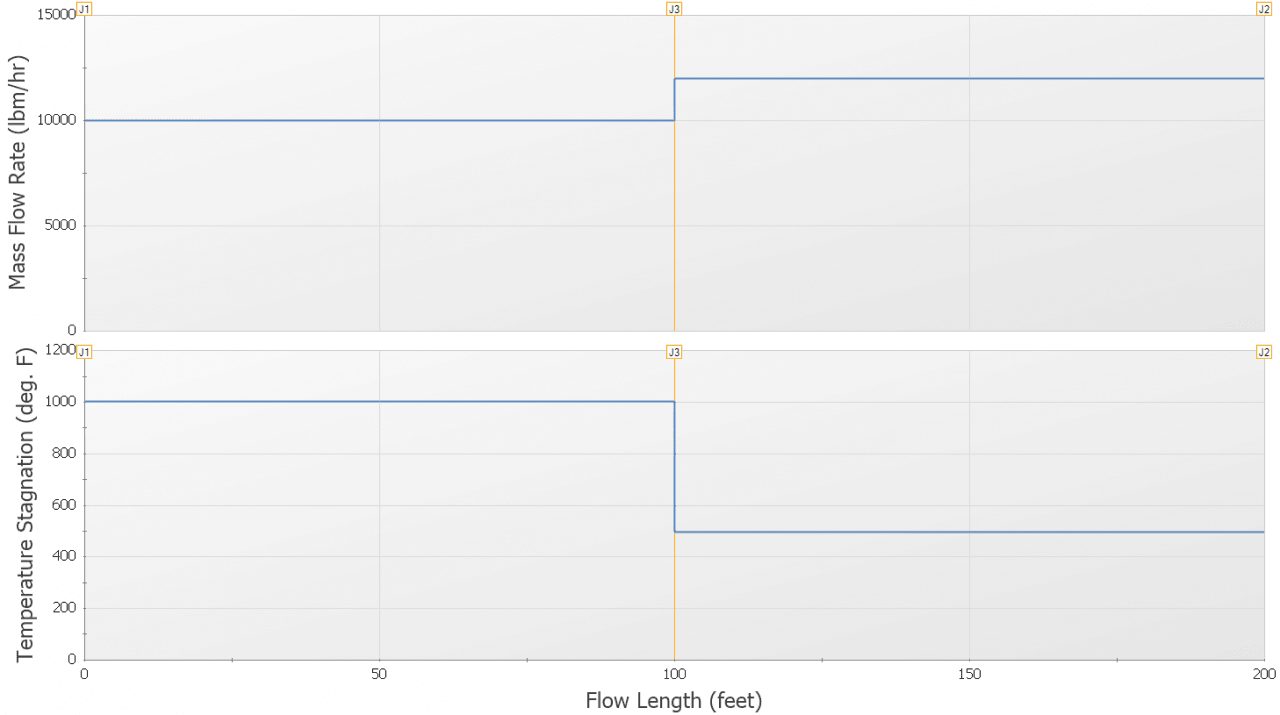
Is this temperature drop reasonable? To check, you can perform hand calculations:
Eq. 1) m1h1+m2h2=m3h3
Eq. 2) m1+m2=m3
where m is the mass flow rate in lbm/hr and h is the enthalpy in Btu/lbm. State 1 is the inflow of superheated steam, state 2 is the inflow of liquid water from the desuperheater, and state 3 is the cooled steam exiting the desuperheater.
By using the conditions from state 1 and state 2, you can solve these two equations for the enthalpy of the cooled steam (h3). From there, you can use a suitably average specific heat constant to relate the enthalpy to the temperature:
Eq. 3) Δh=cpΔT
which is equivalent to:
Eq. 4) T3=T1+(h3-h1)/cp
where cp is the average specific heat in Btu/lbm-°F.
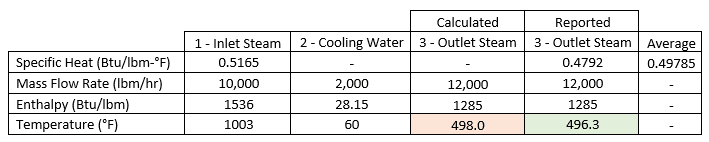
By using these equations, you can confirm that the drop in stagnation temperature caused by the desuperheater is reasonable, as shown in the table below:
Overall, the branch junction is a versatile and powerful tool for modeling. The Flow Source or Sink feature within the branch allows users to model desuperheaters by inputting the mass flow rate and enthalpy of their injection water.