AFT Blog
Applying the Improved ATKF Method for Laminar and Non-Newtonian Flow
If you have worked with Non-Newtonian fluids or low velocity systems in AFT Fathom or AFT Impulse before, then it is likely that you have worked with the Adjusted Turbulent K Factor (ATKF) method before. The ATKF method can be used to adjust K factor data developed for turbulent flow conditions to better predict loss in the laminar flow regime. When a turbulent K factor is not adjusted for laminar conditions, the estimated head loss is often severely under-predicted. Alternative methods to predict pressure loss for minor losses, such as the 3K and equivalent length loss methods, are known to be more conservative than the K factor for calculating the laminar head loss for fittings; However, data for these methods is not as readily available as K factor data. The ATKF method is therefore useful as an approximation. This blog will discuss how the ATKF method has been adjusted to create an Improved ATKF method, and when this method should be applied.
Original ATKF Method
The ATKF method was first established in a technical paper authored by Daniel Wood and Trey Walters titled "Resolving Operational Problems in Pumping Non-Settling Slurries" [1]. The paper explains how the ATKF formula was developed based on the relationship between equivalent length and the K factor from Crane Technical Paper No. 410. The equation is as follows:
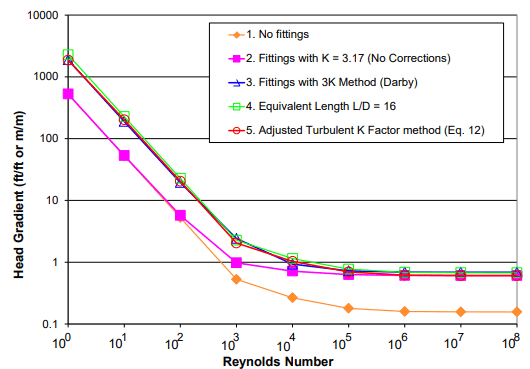
Where Kturbulent is the K factor developed for turbulent flow, flaminar is the friction factor at the current Reynolds number in the system, and fturbulent is the friction factor in the turbulent region. Note that at large Reynolds number values, the friction factor becomes independent of Reynolds number and only depends on the roughness value, as can be seen on the Moody chart for friction factors. In Figure 1 taken from Wood and Walters' technical paper, the agreement between the ATKF, 3K and equivalent length methods can be seen, as compared to the turbulent K factor with no corrections applied. Note that this figure was based off of a test case using 2-inch commercial steel pipe. It can be seen that the ATKF method agrees closely with the 3K and equivalent length methods, while the loss calculated using the turbulent K factor in the laminar region becomes negligible.
ATKF Method with Varied Pipe Roughness
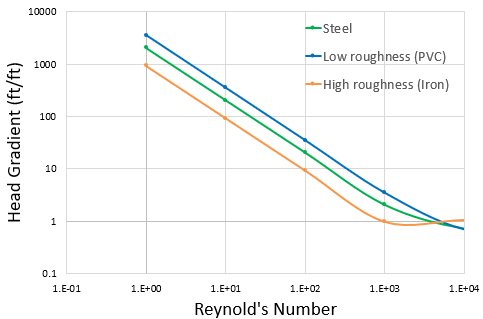
While the ATKF method does work well for commercial steel pipe, it was discovered that the method showed some strange behavior when the pipe roughness was changed. Using an identical pipe with a lower roughness value produced a higher pressure loss, while a larger roughness produced less pressure loss, as can be seen in Figure 2.
This behavior was occurring due to the fact that the ATKF method is inversely related to pipe roughness. As noted earlier, the turbulent friction factor depends on pipe roughness. However, the laminar friction factor only depends on the Reynolds number. By introducing this inverse dependence on the pipe roughness through the turbulent friction factor the K factor was therefore being scaled unexpectedly.
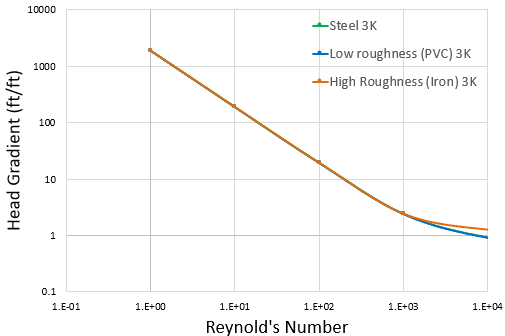
If the 3K method is used, the loss in the laminar region behaves in a more intuitive manner, as can be seen below in Figure 3, where the loss remains constant for varying pipe roughness. Recall that the laminar friction factor does not depend on pipe roughness, so frictional losses in the pipe in the laminar region are also independent of roughness.
Improved ATKF Method
To resolve the observed issues, the dependence on pipe roughness needed to be removed from the ATKF method by using a fixed value of roughness to determine the turbulent friction factor. The Improved ATKF method can then be written as follows, replacing fturbulent with the reference turbulent friction factor, fturbulent,ref :
To mimic the 3K method, the roughness used to calculate fturbulent,ref is the standard roughness of commercial steel, 0.0018 in. This removes the dependence on roughness in the laminar region to better mimic the 3K method.
Using the Improved ATKF Method in AFT Fathom
The Improved ATKF method can be applied to adjust the loss values for most fittings and losses, and allows the ATKF method to be applicable for different values of pipe roughness. However, there are a few situations where the Improved ATKF method should not be applied. If there is already loss data available based on the laminar regime, then the ATKF method should not be applied, as it is only intended to adjust loss values developed under turbulent conditions.
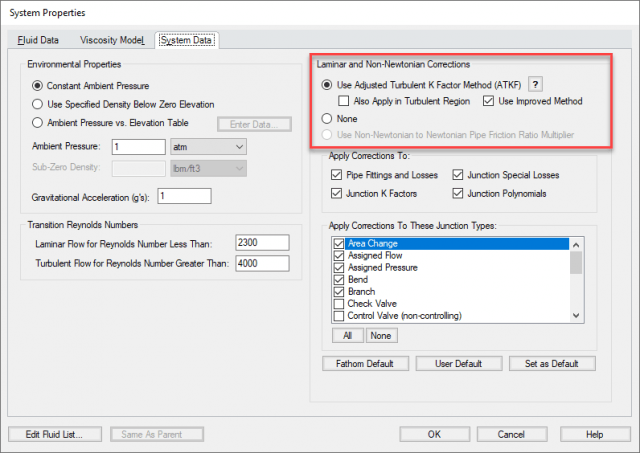
In addition, the Improved ATKF method should only be applied in the laminar region to avoid incorrectly adjusting the losses in the turbulent region. AFT Fathom will automatically turn on the Improved ATKF method to be applied only in the laminar region. These settings can be changed in the System Properties window on the System Data tab (Figure 4). It is possible to selectively apply the ATKF method based off of the junction type in the System Properties window as well.
Using the Improved ATKF method can help to provide a more conservative estimate for fittings and losses when operating in the laminar regime. Make sure that you are applying the Improved ATKF method to avoid operational problems due to insufficient head in your system.
References
[1] D. Wood and T. Walters, "Operational Problems in Pumping Non-Settling Slurries Resolved Using an Improved Laminar Flow Pipe Fitting Loss Model," in Proceedings of the Twenty-Eighth International Pump Users Symposium, September 24 - 27, 2012, Houston, TX, USA, Houston: Turbomachinery Laboratory, Texas A&M University, 2012.




Comments